X 2 y ×3 pts Suppose that the class y= 0 is extremely uncommon (ie, P(y= 0) is small) This means that the classi er f(x) = 1 for all xwill have good risk We may try toWe shall use the identity xy x y = x 2y 2 Here By applying in identity we get Hence the value of is (iv) The given expression is We have So we can express and in the terms of 100 as We shall use the identity xy x y = x 2y 2 Here By applying in
1
(x y)^3 identity class 9
(x y)^3 identity class 9-The perfect cube forms ( x y) 3 (xy)^3 (xy)3 and ( x − y) 3 ( xy)^3 (x −y)3 come up a lot in algebra We will go over how to expand them in the examples below, but you should also take some time to store these forms in memory, since you'll see them often ( x y) 3 = x 3 3 x 2 y 3 x y 2 y 3 ( x − y) 3 = x 3 − 3 x 2 y 3All those who say programming isn't for kids, just haven't met the right mentors yet Join the Demo Class for First Step to Coding Course, specifically designed for students of class 8 to 12 The students will get to learn more about the world of programming in these free classes which will definitely help them in making a wise career choice in the future




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com
(x1) (x2) = x 2 3x 2This video shows how to evaluate using the identity '(xy)3=x3y33x2y3xy2'To view more Educational content, please visit https//wwwyoutubecom/appuserieClass 10 Maths Basic vs Standard;
The algebraic identities for class 9 consist of identities of all the algebraic formulas and expressions You must have learned algebra formulas for class 9, which are mathematical rule expressed in symbols but the algebraic identities represent that the equation is true for all the values of the variables For example;Solution (3x– 4y) 3 is of the form Identity VII where a = 3x and b = 4y So we have, (3x – 4y) 3 = (3x) 3 – (4y) 3 – 3(3x)(4y)(3x – 4y) = 27x 3 – 64y 3 – 108x 2 y 144xy 2 Example 5 Factorize (x 3 8y 3 27z 3 – 18xyz) using standard algebraic identities Solution (x 3 8y 3 27z 3 – 18xyz)is of the form IdentityY 3 ×
Y (7y 9x) (Using ab ac = a (b c)) = 3x2y2 (7y 9x) (ii) a3 – 4a2 12 – 3a = a2 (a – 4) – 3a 12 = a2 (a – 4Class 10 Maths Basic vs Standard;(2x 3) (2x – 3) = (2x) 2 – (3) 2 = 4x 2 – 9




What Is An Identity Shashank Tutorial




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5
NCERT Class 9 Maths Lab Manual – Verify the Algebraic Identity (ab)²Xy 2 z ×On the other hand in expressions like 6 x 8, 5 x 5 y, x2 7 x, x2 3 x 6 we need to determine factors, for which we develop systematic methods to factorise these expressions In the space below we will reduce various forms of algebraic expressions using irreducible factors Example 1 Factorise 21 a2b 27 ab2




Important Questions For Cbse Class 9 Maths Chapter 2 Polynomials




Ncert Solutions Class 9 Maths Chapter 2 Exercise 2 5 Access Free Pdf
We will do questions of these identitiesIdentity VI (a b)3= a3 b3 3ab(a b)Identity VII (a − b)3= a3 b3 3ab(a b)CheckAlgebra Formulasfor full list of formulasLets take an exampleIdentity VI (a b)3= a3 b3 3ab(a b)(2 3)3= 23 33 3(2)(3) (2 3)(5)3= 8 27 18 ×– 3ab (a – b) OBJECTIVE To verify the algebraic identity (a – b)³For example, the identity (x y) 2 = x 2 2 x y y 2 (xy)^2 = x^2 2xy y^2 (x y) 2 = x 2 2 x y y 2 holds for all values of x x x and y y y Since an identity holds for all values of its variables, it is possible to substitute instances of one side of the equality with the other side of the equality Since x − y = 3 xy=3 x




Algebraic Identities Of Polynomials A Plus Topper
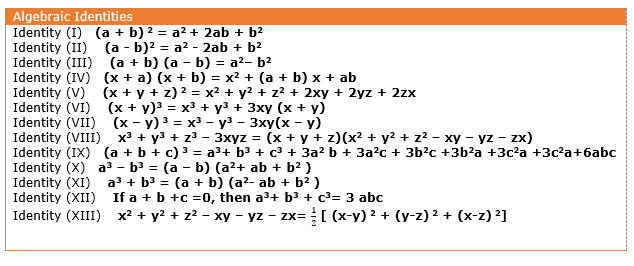



All Useful Algebraic Identities With Proof Examples Physicscatalyst S Blog
Variables (x,y) can take arbitrary values from some domain !5xy 2) sq m = (3 ×In the 4th chapter of Class 9 RD Sharma Solutions students will study important identities as listed below Algebraic Identities Introduction Identity for the square of a trinomial Sum and difference of cubes Identity These books are widely used by the students who wish to




Algebraic Identities Of Polynomials A Plus Topper
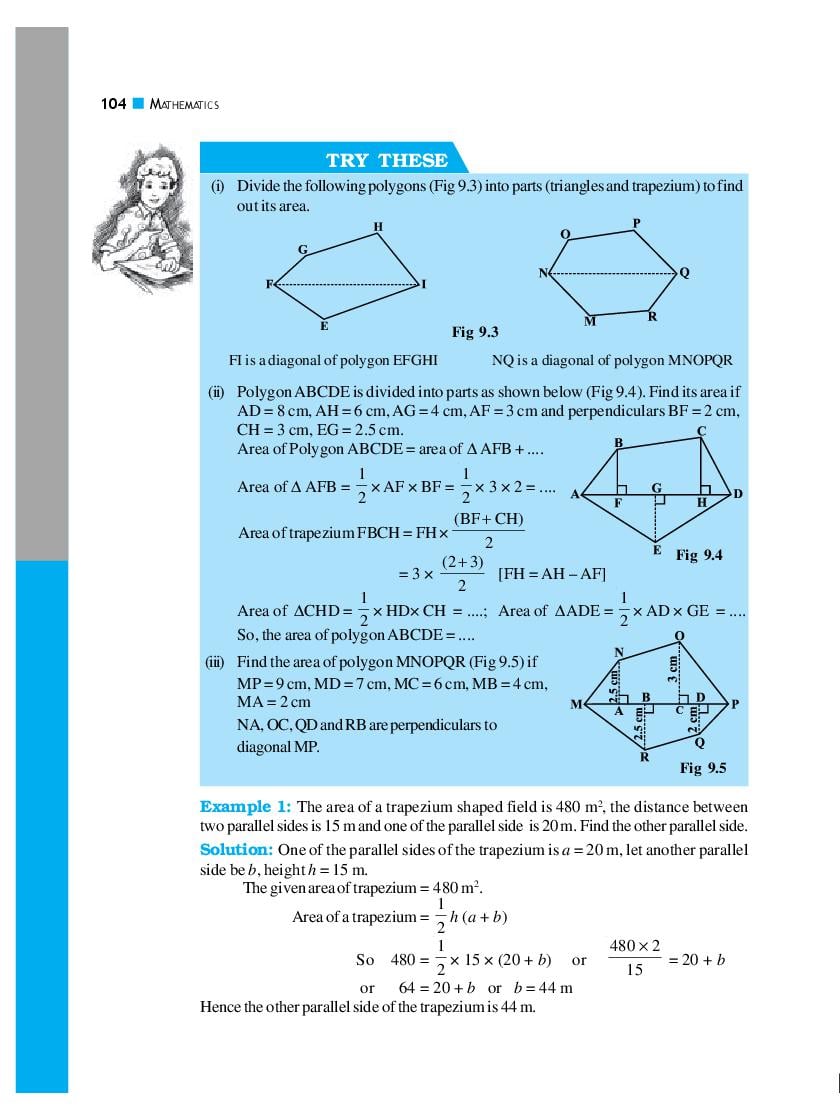



Ncert Book Class 8 Maths Chapter 9 Algebraic Expressions And Identities Aglasem Schools
Y xTy st jjyjj 2 1 CauchySchwarz implies that xTy jjxjjjjyjj jjxjj and y= x jjxjj achieves this bound Proof of (3) We have jjxjj 1 =max y xTy st jjyjj 1 1 So y opt= sign(x) and the optimal value is jjxjj 1 2 Positive semide nite matrices We denote by S n the set of all symmetric (real) n nmatrices 21 De nition De nition 6 A matrixBecause an identity stays the same for every value of its variables, one can substitute the terms of one side of the equation, with the terms of the other side, as shown in the example above, where we replaced an instance of (xy) 2 with the instance of x 2CBSE NCERT Notes Class 9 Maths Polynomials Show Topics Class 9 Maths Polynomials Algebraic Identities Algebraic Identities Algebraic identity is an algebraic equation that is true for all values of the variables occurring in it ( x y) 2 = x2 2 xy y2 ( x – y) 2 = x2 – 2 xy y2 x2 – y2 = ( x y) ( x – y)




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Exercise 2 5




Standard Identities Of Binomials And Trinomials Equations Examples
Still have two truth values for statements (T and F) !Identity VII is a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) Lets take an example a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) 2 3 3 3 4 3 – 3(2)(3)(4) Chapter 3 Class 9 Coordinate Geometry (Term 1) →For class 8 and class 9 standard, these algebraic identities and formulas are commonly used So, this article will be helpful for the students who are appearing for class 8 and class 9 exams Solution By the algebraic identity number 3, we can write the given expression as;




Algebraic Identities For Class 9 Step By Step Guide To Solve Problems




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Mathongo
This is a fairly simple linear differential equation so we'll leave it to you to check that the solution is y ( t) = 1 1 2 e − 4 t − 1 2 e − 2 t y ( t) = 1 1 2 e − 4 t − 1 2 e − 2 t In order to use Euler's Method we first need to rewrite the differentialNCERT Solution For Class 9 Maths Chapter 2 Polynomials Using identity, (xyz)2 = x2y2z22xy2yz2zx Here, x = (1/4)a y = (1/2)b z = 1 5 Factorize (i) 4x29y216z212xy–24yz–16xz (ii) 2x2y28z2–2√2xy4√2yz–8xz SolutionQ4 Expand each of the following, using suitable identities (i) (x 2y 4z) 2 (ii) (2x – y z) 2 (iii) (–2x 3y 2z) 2 (iv) (3a – 7b – c) 2 (v) (–2x




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Chapter 4 Algebraic Identities Rd Sharma Solutions For Class 9 Mathematics Cbse Topperlearning
Cout = XY (X xor Y) CinClass 9 RD Sharma Solutions Chapter 4 Algebraic Identities Ex 43 Question 1 Find the cube of each of the following binomial expressions Solution Question 2 If a b = 10 and ab = 21, find the value of a 3 b 3 Solution a b = 10, ab = 21Polynomials Exercise 25 Part 1 Question 1 Use suitable identities to find the following products (i) `(x 4)(x 10)` Answer Given, `(x 4)(x 10)` We




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Exercise 2 5



1
CBSE Sample Papers 2122 (Term 1) New;This algebraic identity can be written in the following form too ( a − b) 3 = a 3 − b 3 − 3 a 2 b 3 a b 2 Generally, the a minus b whole cubed algebraic identity is called by the following three ways in mathematics The cube of difference between two terms identity or simply the cube of difference identity The cube of a binomial formulaX 2 yz Solution Question 9 Find the area of the rectangle whose length and breadths are 3x 2 y m and 5xy 2 m respectively Solution Length = 3x 2 y m, breadth = 5xy 2 m Area of rectangle = Length ×




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com



1
NCERT Class 9 Maths Lab Manual – Verify the Algebraic Identity (a – b)³Get FREE NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Exercise 25 We have created Step by Step solutions for Class 9 maths to help you to revise the complete Syllabus and Score More marks Using identity (xy) 3 =x 3y 3 3xy(xy) = 8a 327b 318ab(2a3b) = 8a 3 – 27 b 3 – 36a 2 b 54ab 2 =8a 3 – 36a 2 b 54ab 2– 3ab (a – b) Materials Required Geometry box Acrylic sheet Scissors Adhesive/Adhesive tape Cutter




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials




Telangana Scert Class 9 Math Solution Chapter 2 Polynomials And Factorisation Exercise 2 5
Breadth = (3x 2 y ×Materials Required Drawing sheet Pencil Cellotape Coloured papers Cutter Ruler Prerequisite Knowledge Square and its area Rectangle and its area Theory A square is a quadrilateral whose allOBJECTIVE To verify the algebraic identity (ab)²
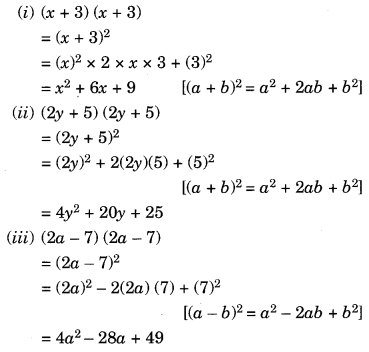



Class 8 Ex 9 5 Maths Ncert Solutions




Ex 9 5 3 Find The Squares Xy 3z 2 Using The Algebra Identities
(x y) 3 = x 3 3x 2 y 3xy 2 y 3 Example (1 a 2 ) 3 = 1 3 31 2 a 2 31(a 2 ) 2 (a 2 ) 3 = 1 3a 2 3a 4 a 6 (x y z) 2 = x 2 y 2 z 2 2xy 2xz 2yzWhen we assign values to x and y, then P has a truth valueTranscript Ex 25, 9 Verify (i) x3 y3 = (x y) (x2 – xy y2) LHS x3 y3 We know (x y)3 = x3 y3 3xy (x y) So, x3 y3 = (x y)3 – 3xy (x y




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf




Ex 9 3 3 Find The Product I A 2 2a 22 4a 26 Algebra
State whether the following statements are true or false Give reasons to justify your answers (a) The degree of polynomial 5 x5 6 x4 8 x2 is 4 (b) The algebraic expression is a polynomial (c) The polynomial is a quadratic trinomial Using the long division method, determine the remainder when the polynomial 4 x5 2 x4 x3 4 x2 7Class 6 Maths (with MCQs) Class 7 Maths (with MCQs) Class 8 Maths (with MCQs) Class 9 Maths (with MCQs) Class 10 Maths (with MCQs) Class 11 Maths (with MCQs) Class 12 Maths (with MCQs) NCERT Solutions Science;Example 12 Factorise the following (i) 21x2y3 27x3y2 (ii) a3 – 4a2 12 – 3a (iii) 4x2 – x 25 (iv) 2 –9 9 y (v) x4 – 256 Solution (i) 21x2y3 27x3y2 = 3 ×



Cbse Class 8 Mathematics Algebraic Identities Bridge Course Worksheet




Polynomials Ppt Video Online Download
Theorem 36 Let F be any partition of the set S Define a relation on S by x R y iff there is a set in F which contains both x and y Then R is an equivalence relation and the equivalence classes of R are the sets of F Pf Since F is a partition, for each x in S there is one (and only one) set of FThe trigonometry formulas for class 10 pdf covers the basic trigonometric functions for a rightangled triangle ie Sine (sin), Cosine (cos), and Tangent (tan) which can be used to derive Cosecant (cos), Secant (sec), and Cotangent (cot) The formulas of trigonometry class 10 are listed belowAlgebra formulas for class 9 include formulas related to algebra identities or expressions Algebraic identities chapter is introduced in CBSE class 9 This is a tricky chapter where one needs to learn all the formula and apply them accordingly To make it easy for them, BYJU'S provide all the formulas on a single page ( x^{3} y^{3




Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks




Class 9 Cbse Posts Facebook
CBSE Sample Papers 2122 (Term 1) New;We shall use the identity xy x y = x 2y 2 Here By applying in identity we get Hence the value of is (iv) The given expression is We have So we can express and in the terms of 100 as We shall use the identity xy x y = x 2y 2 Here By applying inClass 6 Maths (with MCQs) Class 7 Maths (with MCQs) Class 8 Maths (with MCQs) Class 9 Maths (with MCQs) Class 10 Maths (with MCQs) Class 11 Maths (with MCQs) Class 12 Maths (with MCQs) NCERT Solutions Science;




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Ex 9 4 Ncert Solutions
Answer In the given problem, we have to simplify the value of each expression (i) Given We shall use the identity for each bracket x 2 2 y 3 2 z 4 2 2 x 2 y 3 2 y 3 z 4 2 x 2 z 4 By arranging the like terms we get Now adding or subtracting like terms, Hence the value ofThe document Algebraic Identities Polynomials, Class 9, Mathematics EduRev Notes is a part of Class 9 category All you need of Class 9 at this link Class 9 ALGEBRAIC IDENTITIES Let us recall the following algebraic identities is earlier (a b) 2 = a 2 2ab b 2 (a – b) 2 = a 2 – 2ab b 2 (a b) (a – b) = a 2 – b 2Sample Papers Class 10 Solution Maths New




Algebra Formulas For Class 9 Pdf Download Free Here




Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities
Sample Papers Class 10 Solution Maths NewMultiply the following expressions (a) 3xy 2 ×A predicate P describes a relation or property !



Algebraic Formula




Class 9th Maths Chapter 2 Polynomials Learner S Institute
Y = 3 ×5125 = 8 27 9Time invariant system, given an input x(t) x y H We can write a signal x(t) as a sample of itself x(t) = Z 1 1 x(˝) ˝(t) d˝ This means that x(t) can be written as a weighted integral of functions Cu (Lecture 3) ELE 301 Signals and Systems Fall 1112 9 / 55 Applying the system H to the input x(t), y(t) = H(x(t)) = H Z 1 1 x(˝) ˝(t)d˝




Chapter 4 Algebraic Identities Rd Sharma Solutions For Class 9 Mathematics Cbse Topperlearning




Rd Sharma Class 9 Solutions Chapter 4 Algebraic Identities
NCERT Solution For Class 9 Maths Chapter 2 Polynomials Exercise 25 Page 48 1 Use suitable identities to find the following products Here, the identity, 3 (x y) = x 3 y 3 3xy (x y) is used (ii) 8a 3 –b 3 –12a 2 b6ab 2 Solution The expression, 8a 3 –b 3 −12a 2 b6ab 2 2can be written as (2a) –b 3 –3Algebraic Identities Cubic Type ,Polynomials Get topics notes, Online test, Video lectures, Doubts and Solutions for CBSE Class 9 on TopperLearningCBSE Class 8 Math Algebraic Identities Part 3 Identity 2 Solved QuestionsDAVFor better understanding of solving questions, look for playlisthttps//ww




Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Ex 9 5 Cbsetuts Com




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf
(a)x39 x2 23x15 (b) x36 x2 11x6 Q3 Factorize the following by using a suitable identity (a) 4x2 12xy 9y2 (b) 2a5 – 54 a2 (c) 22x3 3 3 y3 (d) x5 x (e) x6 – y6 (f) (ab)3 (bc)3 (ca)3 (f) x8y8 (g) 27x3135x2 225x 125 Q4 Evaluate the following using a suitable identityTABLE 39 and FIGURE 311 The Truth Table and The Logic Diagram for a HalfAdder Note that this fulladder is composed of two halfadder FIGURE 312 The Truth Table and The Logic Diagram for a FullAdder Sum = X xor Y xor Cin;X 3, 2y – 5, 3x2, 4xy 7 etc You can form many more expressions As you know expressions are formed from variables and constants The expression 2 y – 5 is formed from the variable y and constants 2 and 5 The expression 4 xy 7 is formed from variables x and y and constants 4 and 7




Rd Sharma Solutions Class 9 Chapter 4 Algebraic Identities Updated For 21 22




Chapter 4 Expansion Selina Concise Mathematics Part I Solutions For Class 9 Mathematics Icse Topperlearning
Explanation (x −y)3 = (x − y)(x −y)(x −y) Expand the first two brackets (x −y)(x − y) = x2 −xy −xy y2 ⇒ x2 y2 − 2xy Multiply the result by the last two brackets (x2 y2 −2xy)(x − y) = x3 − x2y xy2 − y3 −2x2y 2xy2 ⇒ x3 −y3 − 3x2y 3xy2 Always expand each term in the bracket by all the otherWe already have an identity for (x y) 3 So, let's try to derive the identity x 3 y 3 using the identity for (x y) 3 Let's first try to understand this geometrically Let's join our cubes as shown above We arranged both cubes in such a way to convert it into a cube as shown above(5x 2 y) (b) x 2 yz ×




Ncert Solutions For Class 8 Maths Algebraic Expressions And Identities




Ex 2 5 3 I Factorise 9x2 6xy Y2 Using Appropriate Identities




Ncert Solutions Class 9 Maths Chapter 2 Exercise 2 5 Access Free Pdf




Factorization Of Polynomials Class 9 Ex 2 5 Q13 Ncert Algebraic Identities Solution Ncer Youtube




X Y 3 X3 Y3 3xy X Y Brainly In




Ncert Solutions For Class 8 Maths Algebraic Expressions And Identities




Ncert Solutions For Class 8 Mathematics Chapter 9 Algebraic Expressions And Identities Exercise 9 5




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Mathongo




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes



Algebra Formula Chart




Selina Concise Mathematics Class 8 Icse Solutions Chapter 12 Algebraic Identities Cbse Tuts
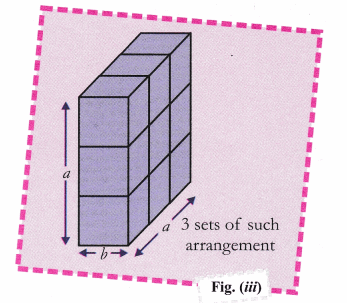



Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2 Cbse Sample Papers




Exercise 25 Question 1 Use Suitable Identities To Find The Following Products X 4 X 10x 8x 10 I 3 3 3x 43x 5 Iii 2 Iv 3 2x 3 2x V Answer I By Using The Identity X Ax B X A B
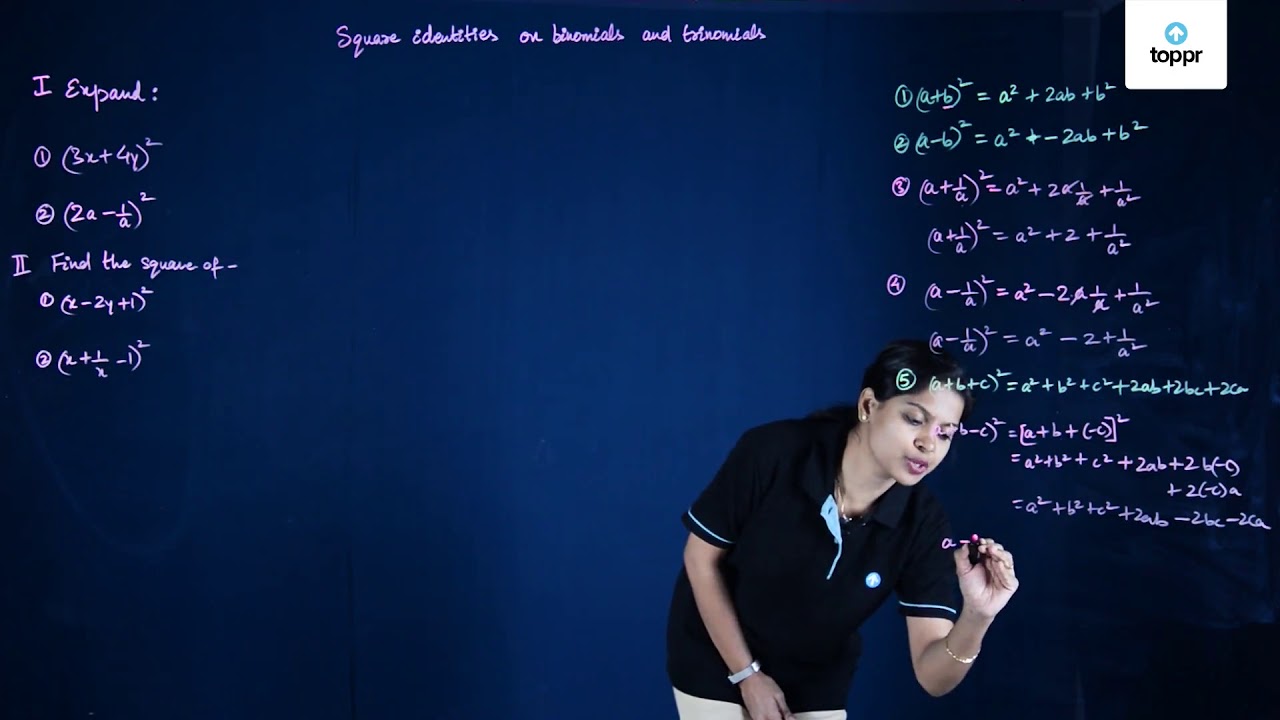



Standard Identities Of Binomials And Trinomials Equations Examples




Algebra Formulas For Class 9 Pdf Download Free Here




Ncert Solutions Class 9 Maths Chapter 2 Polynomial Updated For 21




Ncert Solutions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities




Polynomials Class 9 Extra Questions Maths Chapter 2 Learn Cbse



Identity Mathematics Wikipedia




Ncert Solutions Class 9 Maths Chapter 2 Exercise 2 5 Access Free Pdf




How To Verify Algebric Identity X Y 3 X3 3xy X Y Y3 Maths Polynomials Meritnation Com
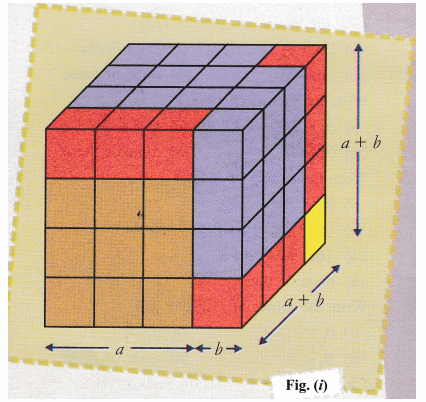



Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2 Cbse Sample Papers




Cbse Class 9 Algebraic Identities Offered By Unacademy




Ncert Solutions For Class 8 Maths Algebraic Expressions And Identities Ex 9 4 Algebraic Expressions Class 8 Math



What Is The Formula Of Math A B 3 Math Quora




Rd Sharma Class 9 Solutions Chapter 5 Factorisation Of Algebraic Expressions Exercise 5 1




Rd Sharma Class 9 Solutions Algebraic Identities Exercise 4 3 8 Rdsharmaclass9 Class9solutions Rdsharmaclass9solutions Rd Math Notes Solutions Class




Cbse Class 9 Maths Lab Manual Algebraic Identity A3 A B Ab B2 Cbse Sample Papers




Ex 9 4 3 Vi Simplify X Y X 2 Xy Y 2 Chapter 9 Class 8




Chapter 4 Algebraic Identities Rd Sharma Solutions For Class 9 Mathematics Cbse Topperlearning




Ncert Maths Solutions Chapter 2 Polynomials Exercise 2 5




5 Extra Questions For Class 9 Maths Chapter 2 With Solution Polynomials Zeroes Remainder Theorem Factorization And Algebraic Identities




Algebraic Identities Of Polynomials A Plus Topper




Ex 2 5 9 Verify I X 3 Y 3 X Y X 2 Xy Y 2 Teachoo




Class 9ncert Solutionschapter 2 Polynomialsexercise 2 5 Solve All Questions And Give Me Answersplease Brainly In




Ncert Solution For Class 8 Exercise 9 5 Chapter 9 Algebraic Expressions And Identities Pathanto




Assignment On Algebraic Identities Pdf



Ncert Solutions Class 8 Mathematics Algebraic Expressions And Identities




Chapter 2 Polynomials Ncert Solutions Class 9 Maths




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Class 9 Maths Worksheet 6 16 July 21 English Medium Maths Worksheet 6 Class 9 Worksheet 6 Youtube




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf




Ncert Solutions For Class 9 Maths Exercise 2 5 Chapter 2 Polynomials Study Path




Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Ex 2 5 Cbsetuts Com




Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes




Polynomials Important Questions Of Identities Algebraic Identities Class 9 Oda Class Youtube



Rd Sharma Solutions Class 9 Chapter 3 Rationalisation




Ex 2 5 11 Factorise 27 X3 Y3 Z3 9xyz Class 9 Ex 2 5




Cbse Revision Notes For Class 8 Chapter 9 Algebraic Expressions And Identities




Notes Of Ch 2 Polynomials Class 9th Math




Ncert Solutions For Class 9 Maths Chapter 2 Vidyakul




Class 9ncert Solutionschapter 2 Polynomialsexercise 2 5 Solve All Questions And Give Me Answersplease Brainly In




Ex 2 5 Ques 1 To 5 18th May




Polynomials Class 9 Notes Maths Chapter 2 Learn Cbse




Rd Sharma Class 9 Solutions Algebraic Identities Exercise Flickr




Algebraic Identities Rd Sharma Class 9 Solutions Exercise 4 5




Kseeb Solutions For Class 9 Maths Chapter 4 Polynomials Ex 4 5 Kseeb Solutions




Important Questions For Class 8 Maths Chapter 9 Algebraic Expressions And Identities Free Pdf
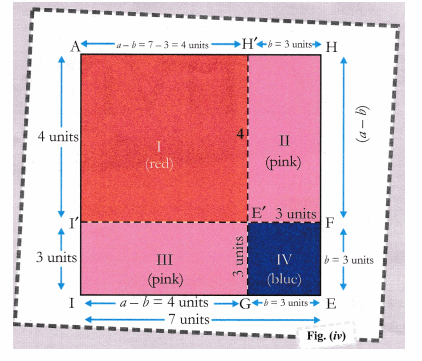



Cbse Class 9 Maths Lab Manual Algebraic Identity A B 2 2ab B2 Cbse Sample Papers




Questions On Algebraic Expressions Algebraic Identities Algebraic Formulas
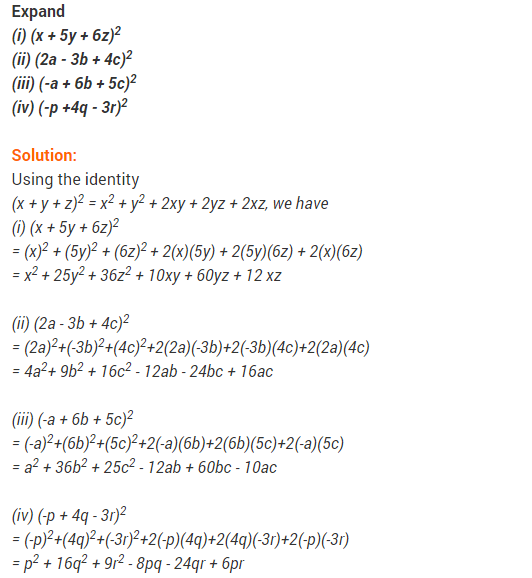



Polynomials Class 9 Extra Questions Maths Chapter 2 Learn Cbse




Algebraic Identities Of Polynomials A Plus Topper
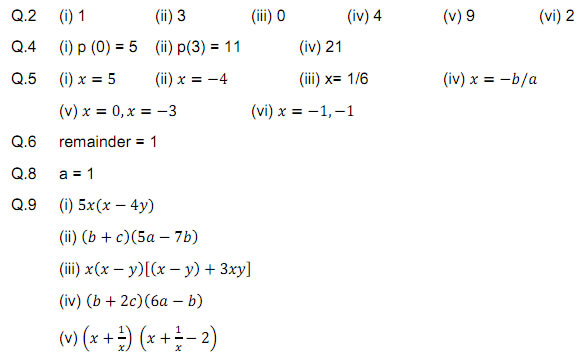



Polynomials Class 9 Maths Notes With Formulas Download In Pdf




Ncert Maths Solutions Chapter 2 Polynomials Exercise 2 5



0 件のコメント:
コメントを投稿